Cache: a place for concealment and safekeeping
This post shows briefly how CPU caches are organized in modern Intel processors. Cache discussions often lack concrete examples, obfuscating the simple concepts involved. Or maybe my pretty little head is slow. At any rate, here’s half the story on how a Core 2 L1 cache is accessed:
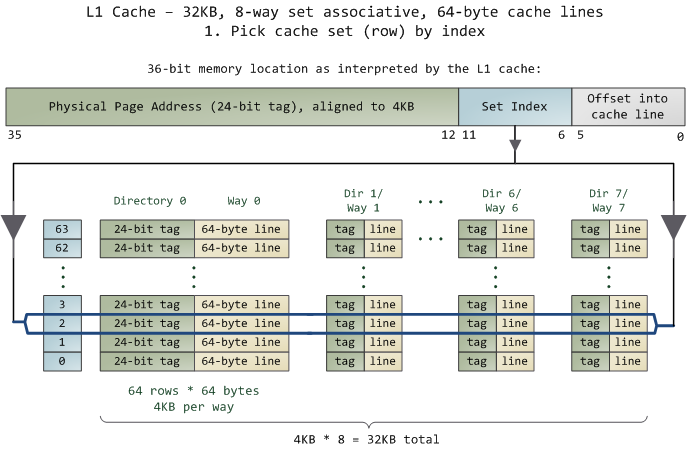
The unit of data in the cache is the line, which is just a contiguous chunk of bytes in memory. This cache uses 64-byte lines. The lines are stored in cache banks or ways, and each way has a dedicated directory to store its housekeeping information. You can imagine each way and its directory as columns in a spreadsheet, in which case the rows are the sets. Then each cell in the way column contains a cache line, tracked by the corresponding cell in the directory. This particular cache has 64 sets and 8 ways, hence 512 cells to store cache lines, which adds up to 32KB of space.
In this cache’s view of the world, physical memory is divided into 4KB physical pages. Each page has 4KB / 64 bytes == 64 cache lines in it. When you look at a 4KB page, bytes 0 through 63 within that page are in the first cache line, bytes 64-127 in the second cache line, and so on. The pattern repeats for each page, so the 3rd line in page 0 is different than the 3rd line in page 1.
In a fully associative cache any line in memory can be stored in any of the cache cells. This makes storage flexible, but it becomes expensive to search for cells when accessing them. Since the L1 and L2 caches operate under tight constraints of power consumption, physical space, and speed, a fully associative cache is not a good trade off in most scenarios.
Instead, this cache is set associative, which means that a given line in memory can only be stored in one specific set (or row) shown above. So the first line of any physical page (bytes 0-63 within a page) must be stored in row 0, the second line in row 1, etc. Each row has 8 cells available to store the cache lines it is associated with, making this an 8-way associative set. When looking at a memory address, bits 11-6 determine the line number within the 4KB page and therefore the set to be used. For example, physical address 0x800010a0 has 000010 in those bits so it must be stored in set 2.
But we still have the problem of finding which cell in the row holds the data, if any. That’s where the directory comes in. Each cached line is tagged by its corresponding directory cell; the tag is simply the number for the page where the line came from. The processor can address 64GB of physical RAM, so there are 64GB / 4KB == 224 of these pages and thus we need 24 bits for our tag. Our example physical address 0x800010a0 corresponds to page number 524,289. Here’s the second half of the story:
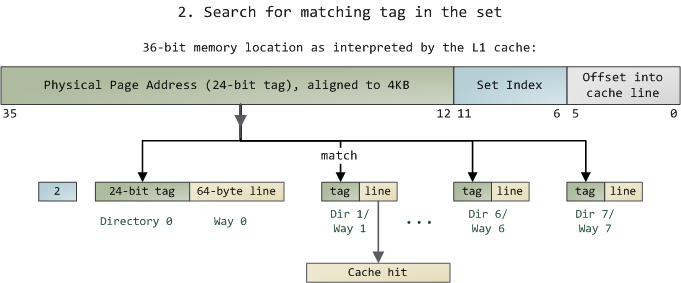
Since we only need to look in one set of 8 ways, the tag matching is very fast; in fact, electrically all tags are compared simultaneously, which I tried to show with the arrows. If there’s a valid cache line with a matching tag, we have a cache hit. Otherwise, the request is forwarded to the L2 cache, and failing that to main system memory. Intel builds large L2 caches by playing with the size and quantity of the ways, but the design is the same. For example, you could turn this into a 64KB cache by adding 8 more ways. Then increase the number of sets to 4096 and each way can store 256KB. These two modifications would deliver a 4MB L2 cache. In this scenario, you’d need 18 bits for the tags and 12 for the set index; the physical page size used by the cache is equal to its way size.
If a set fills up, then a cache line must be evicted before another one can be stored. To avoid this, performance-sensitive programs try to organize their data so that memory accesses are evenly spread among cache lines. For example, suppose a program has an array of 512-byte objects such that some objects are 4KB apart in memory. Fields in these objects fall into the same lines and compete for the same cache set. If the program frequently accesses a given field (e.g., the vtable by calling a virtual method), the set will likely fill up and the cache will start trashing as lines are repeatedly evicted and later reloaded. Our example L1 cache can only hold the vtables for 8 of these objects due to set size. This is the cost of the set associativity trade-off: we can get cache misses due to set conflicts even when overall cache usage is not heavy. However, due to the relative speeds in a computer, most apps don’t need to worry about this anyway.
A memory access usually starts with a linear (virtual) address, so the L1 cache relies on the paging unit to obtain the physical page address used for the cache tags. By contrast, the set index comes from the least significant bits of the linear address and is used without translation (bits 11-6 in our example). Hence the L1 cache is physically tagged but virtually indexed, helping the CPU to parallelize lookup operations. Because the L1 way is never bigger than an MMU page, a given physical memory location is guaranteed to be associated with the same set even with virtual indexing. L2 caches, on the other hand, must be physically tagged and physically indexed because their way size can be bigger than MMU pages. But then again, by the time a request gets to the L2 cache the physical address was already resolved by the L1 cache, so it works out nicely.
Finally, a directory cell also stores the state of its corresponding cached line. A line in the L1 code cache is either Invalid or Shared (which means valid, really). In the L1 data cache and the L2 cache, a line can be in any of the 4 MESI states: Modified, Exclusive, Shared, or Invalid. Intel caches are inclusive: the contents of the L1 cache are duplicated in the L2 cache. These states will play a part in later posts about threading, locking, and that kind of stuff. Next time we’ll look at the front side bus and how memory access really works. This is going to be memory week.
Update: Dave brought up direct-mapped caches in a comment below. They’re basically a special case of set-associative caches that have only one way. In the trade-off spectrum, they’re the opposite of fully associative caches: blazing fast access, lots of conflict misses.
January 11, 2009 at 11:11 pm | Filed Under Internals, Software Illustrated
Subscribe to blog
Comments
24 Responses to “Cache: a place for concealment and safekeeping”
Leave a Reply
Very nice I love all your “Internals” posts, one simple question, what do you use to make the schemas?
Thank you.
Peter: I’m using Visio 2007. I use ‘themes’, which is a nice way to apply common fills and lines to the shapes (like rounding, gradients, that kind of thing). The font is Consolas 10 pt. Cheers.
You might also point out that in addition to fully-associated and set-associative, caches can also be direct-mapped. Direct mapping just uses the low bits of the address to select the *exact* location the data could possibly be (essentially a single set). It’s very simple and fast, but only one line can map to a given index, so you can have issues where cache lines fight each other to be kept in cache. This can create big problems when doing things like data copies from one region of memory to another where the distance between the copies is a multiple of the cache size.
In reality, set-associative caches are the mid-way point between fully-associative and direct-mapped. They try to gain some of the benefits of full associativity while managing the complexity/power/performance.
Nice description, though.
@Dave: thanks!
[...] Cache: a place for concealment and safekeeping : Gustavo Duarte (tags: reference programming hardware architecture optimization memory cache cpu processor intel) [...]
[...] deterministic. Also, the constant reuse of stack regions tends to keep active stack memory in the cpu caches, speeding up access. Each thread in a process gets its own [...]
[...] deterministic. Also, the constant reuse of stack regions tends to keep active stack memory in the cpu caches, speeding up access. Each thread in a process gets its own [...]
[...] Dave brought up direct-mapped caches in a comment below. They’re basically a special case of set-associative caches that have only one way. In the [...]
Great Post… nicely written. I used to hear that we should write code to utilize the cache’s effectively ? I know using arrays we could achieve good locality. Could you please provide some insight on how we code affects the I-cache and how our datastructures could use D-cache effectively.
[...] deterministic. Also, the constant reuse of stack regions tends to keep active stack memory in the cpu caches, speeding up access. Each thread in a process gets its own [...]
@maverick: Check Ulrich Drepper’s paper, “What Every Programmer Should Know About Memory”. It’s the best concise resource on this that I know of.
[...] Dave brought up direct-mapped caches in a comment below. They’re basically a special case of set-associative caches that have only one way. In the [...]
[...] deterministic. Also, the constant reuse of stack regions tends to keep active stack memory in the cpu caches, speeding up access. Each thread in a process gets its own [...]
Great informative post. I clarified many things which weren’t as clearly explained in other sources I read.
I do have one small thing I couldn’t understand related to virtual indexing:
“Because the L1 way is never bigger than an MMU page, a given physical memory location is guaranteed to be associated with the same set even with virtual indexing.”
First of all, I’m not quite sure what the MMU page is. As far as I know, the MMU is what “magically” takes care of the virtual to physical address translation, using the page table and its “cache” – the TLB.
So, why would the bits 11-6 in the virtual address be ok to use for indexing instead of bits 11-6 in the physical address. Could you please clarify this for me ?
Thanks and keep up the good work !
[...] about cache architecture itself, it’s a topic on its own. If you’re interested see Gustavo’s article or this paper by Ulrich Drepper. In a nutshell – cache is a very fast memory organized in lines [...]
[...] 进程地址空间的首段地址便是栈，它储存了局部变量以及大多数编程语言的函数参数。当调用方法或者函数时，会有一个新的元素进栈。一旦函数返回了值，那么该元素就会被销毁。这种简单的设计，很有可能是考虑到数据操作都符合后进先出（LIFO ）规则，这意味着访问栈的内容并不需要复杂的数据结构，一个简单的栈顶指针就能搞定一切。进栈和出栈的操作方便快捷，不需要过多判断。另外，栈的反复使用能够使栈主流在CPU缓存（cpu caches）中，从而加快数据存取。每个进程中的每个线程都有属于自己的栈。 [...]
Terrific Gustavo Duarte , no words to say .
You have done a excellent job .
Keep it up.
Many thanks
Narendra
[...] Good overview of caching: http://duartes.org/gustavo/blog/post/intel-cpu-caches [...]
Splendid way of explaining things. I must say that your blog on x86/AMD64 and related technology is one of the best someone can read. Thanks.
Reyaz A.
[...] 进程地址空间的首段地址便是栈，它储存了局部变量以及大多数编程语言的函数参数。当调用方法或者函数时，会有一个新的元素进栈。一旦函数返回了值，那么该元素就会被销毁。这种简单的设计，很有可能是考虑到数据操作都符合后进先出（LIFO ）规则，这意味着访问栈的内容并不需要复杂的数据结构，一个简单的栈顶指针就能搞定一切。进栈和出栈的操作方便快捷，不需要过多判断。另外，栈的反复使用能够使栈驻留在CPU缓存（cpu caches）中，从而加快数据存取。每个进程中的每个线程都有属于自己的栈。 [...]
can you discuss about the 2-way set associative cache to 8-way set associative cache?
thank you!
Your blog triggered some thoughts about OS design issues related to caching. In my hobby OS I create “Thread” objects of size 4K (i.e. exactly one page), which contains some fields that are accessed each scheduling quantum. One of these fields is the SSE state information (512 bytes) which must be aligned by 512 bytes (or an exception occurs)
The above design would allow at most 8 concurrent active threads before cache trashing kicks in. This can be increased to 64 by allocating the SSE state memory outside of the Thread structure (i.e. varying its offset by 512 instead of 4K), and adding a cache optimization delta of n*64 bytes to vary the offsets of the fields
[...] Gustavo’s article 或 this paper by Ulrich [...]
[...] deterministic. Also, the constant reuse of stack regions tends to keep active stack memory in the cpu caches, speeding up access. Each thread in a process gets its own [...]