Counting Infinity
Infinity is a fascinating idea and it is behind some of the most beautiful results in mathematics. Much of this beauty is accessible to everyone, brought to us by the brilliant Georg Cantor using simple arguments that require little math. I hope to show some of this goodness to people who haven’t seen it before. Here we go.
Imagine a shepherd tending a flock of a few dozen sheep. In the morning, the sheep get out of the farm to do sheepish things. In the evening, the shepherd wants to make sure he got all his sheep back. One problem: he can’t count. What’s a shepherd to do? One solution would be to keep track of the sheep as they go out. For example, he could throw a pebble into a bucket for each sheep leaving the farm. In the evening, a pebble goes out for each returned sheep. At any given time, the number of pebbles in the bucket is exactly equal to that of outstanding sheep. You can picture the sets of sheep and pebbles like so:
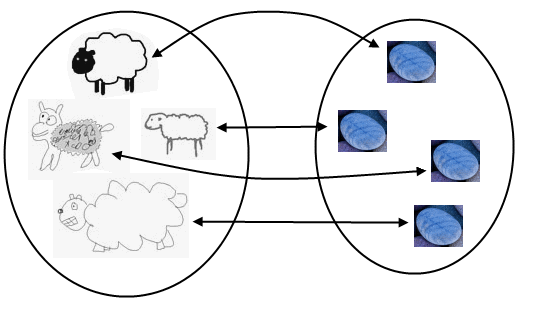
Each sheep is paired with a distinct pebble and there are no left overs on either side. In set theory this is a bijection. Even though the sheep have not been counted, we know the sets have the same number of elements. They are equivalent in a way, not because you eat pebbles or throw sheep, though I suppose you could, but because of the bijection. If you accept this premise, which is reasonable enough, then you’re in for some fun. Interesting things happen when we use bijections to compare sets nobody can count: the infinite sets. For example, let’s compare the natural numbers (1, 2, 3…) to the even natural numbers (2, 4, 6…). It sounds like we should have less even numbers, but lo and behold, we get this:
Every natural number has been paired with a distinct even number. No left overs. Strangely, these sets are equivalent. It turns out many sets are equivalent to the natural numbers; we call these sets denumerable. For example, the set of Turing Machines is denumerable because there are infinitely many machines and they can each be fully described by a distinct natural number. The integers are yet another example:
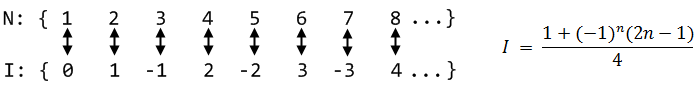
Some people see these results as trivial: their intuitive notion is that any “infinity” must be the same. Others see a paradox. How can a part of something be equivalent to the whole? Let’s try to give everyone a paradox by finding a set that is not denumerable. How about the rationals? Surely there must be more fractions than natural numbers! Right? Cantor probably thought so, until he discovered a procedure to enumerate the rationals:
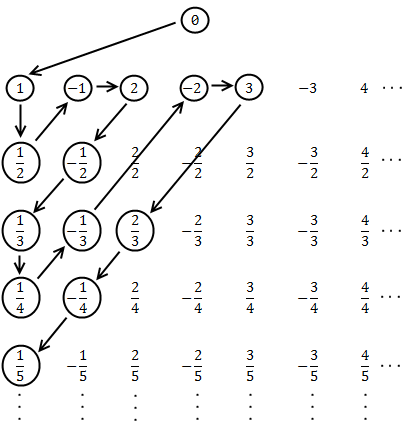
Starting at the top and following the pattern, this procedure hits each rational number once. As it moves along, we can associate successive natural numbers with each hit. Here are the first few pairings:
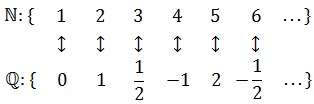
It is pretty clear that the arrangement above covers all of the rationals, but the crucial point is that Cantor’s pattern will reach any given rational in a finite number of steps. The zigzag is important: if we go off in a single direction (say, across the first row to the right) then we get stuck in the infinitude of that row alone, and there would be rationals left over. The zigzag delivers us from that evil. This argument does not produce an equation for a bijection, but since it builds a listing that contains every rational number, it shows they are denumerable. Conversely, if a set is denumerable its elements can be put into a listing where each element is paired with a natural number.
(As an aside, the 1999 paper Recounting the rationals establishes a precise bijection by using a tree to generate all fractions in reduced form. The tree has all sorts of magical properties, cool stuff. It’s an accessible paper, plus Brent Yorgey wrote a great walk through of it.)
All of our sets so far have been denumerable, except for the sheep who were finite. At this point, Cantor might have wondered if maybe there is only one infinity. But then again, if you build a number line using the sets we have seen so far, you end up with holes. The naturals are mere dots on the number line, most fractions fall in a hole:
The rationals, on the other hand, are dense. Between any two given rationals, there is another rational (an infinite number of them actually). Yet the rational number line also has holes, which are the irrational numbers. Below is a famous irrational number, on whose account its discoverer was allegedly drowned at sea, shown along the rational number line:
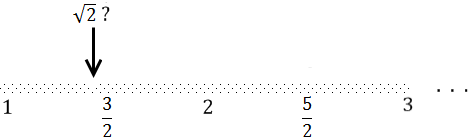
Irrational numbers cannot be expressed as a fraction; moreover, when written out as numbers using positional notation (say, as decimal numbers) their digits never settle into any kind of periodic pattern. Fractions, by contrast, eventually settle into a pattern when written out (e.g., 0.333…, 0.25000…). All of the rationals plus all of the irrational numbers make up the real numbers. And those guys form a number line free of holes. Any point in the number line is a real number, any crazy sequence of digits you come up with is a real number. It’s the continuum. You might get the impression that irrational numbers are rare, oddballs among the familiar rationals, but that’s not the case at all. The sparse number line above is an attempt at visualizing that fact, in addition to showcasing my superior preschool MS Paint skillz. The reals are a vast ocean of irrationals pointed here and there by a fraction, and we’ll see why.
So now Cantor pits the real numbers against the naturals. He shows that even a section of the reals – the interval between 0 and 1 – is not denumerable. He uses a proof by contradiction, which is a common way to show that something cannot be true. It goes like this: suppose there is a way to enumerate the reals between 0 and 1. Then there is a listing containing every real number in that interval, each one associated with a different natural number. It might look like this:
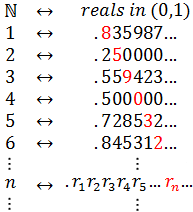
The actual numbers shown above are not important, since the complete list is infinite and has every real number in the interval. Some of the reals up there are clearly rationals and have settled into a periodic pattern (0.250… and 0.500…). The others look pretty random, they could be irrational or maybe they haven’t settled into their periodic patterns yet. Either way, for each number the digits go on indefinitely, rationals in a pattern (possibly of zeros) and irrationals randomly.
Notice how the numbers in red form a diagonal, which is itself infinite. Let’s build a number using that diagonal. Going down the list, for each row we pick a digit that is different than the digit in red. For example, we could add 1 to each digit (9 becomes 0, no carry). You can use any rule as long as the digit is different. Here are the first few digits we get by adding 1 to the red diagonal digits:
The digits of this number p are random and go on infinitely; it is a real number. But due to how we have defined p, it is different from every other number in the list. It differs in at least one digit. Even though the list is infinite, this number is not in it! But then, this list was supposed to have all real numbers so we have a contradiction. Hence our initial assumption must be false; the reals are not denumerable.
The notion of different infinities was a revolutionary one in mathematics. It is a stunning result which ignited the mother of all mathematician flame wars. This was actually the second proof Cantor offered for the non-denumerability of the continuum. The first proof is also valid, but slightly more technical. Cantor’s diagonal argument however is amazingly simple and highly original, as brilliant as its conclusion. It went on to feature prominently in other intellectual landmarks. Alan Turing used it while proving that a Turing Machine cannot predict the behavior of other machines (specifically, predict whether another machine is “cycle-free”, which is now known as the Halting Problem). Gödel used it in his Incompleteness Theorem discussed in Gödel, Escher, Bach. Diagonalization is crucial in recursion theory and complexity theory.
In order to capture these new concepts, Cantor proposed cardinality as a measure of how numerous a set is. A finite set’s cardinality is simply how many elements it has, say 49 for our set of sheep. But the cardinality of an infinite set is expressed by a transfinite number. To make them more esoteric, Cantor used the Hebrew letter aleph for these numbers. By definition, the naturals took aleph zero, 
, for their cardinality. Every denumerable set has cardinality . The cardinality of the reals was defined as c, and Cantor spent years trying to discover whether c = 
, that is, whether the cardinality of the reals is the ‘next bigger one’ after the naturals. So that explains the name in Mona Lisa Overdrive and also the handle for Aleph One, who wrote the classic paper on stack buffer overflows during the Phrack renaissance.
This concludes our first foray into the infinities. There’s way too much to talk about. If there’s interest I’ll write a follow up to see where else infinity leads us. Iterative rather than upfront blogging 
Meanwhile, Journey Through Genius is a great book that does for many theorems, including Cantor’s, what I did on this post. Only much better. Thanks for reading!
January 6, 2009 at 1:07 am | Filed Under CompSci
Subscribe to blog
Comments
29 Responses to “Counting Infinity”
Leave a Reply
Nice article, really liked it. Thanks for sharing
Yes, great article indeed! Math rocks!
Very good explanation, I wish my statistic lectures were this good.
Great article, I wish I were your math-student; I missed some things in school, the void remained there and took its toll on my high-school performance, and that propagated to the university as well.
I keep filling that void, but I know that there is so much stuff out there that is “too high-tech for me”. If you intend to continue this series, there will be a guaranteed audience of >=1 readers (-:
THANK YOU!
Your blog is awesome.
Best regards,
Carlos.
Extremely interesting! Had to read it about 6 times to follow, but that’s because I’ve been reading too many comics lately and not enough good stuff. Found your blog after linked in Lifehacker (I believe?) and have been loving it since. Keep up the great work!
[...] Counting InfinityWhen you have a spare minuteTags: numbers infinity mathematics gustavoduarte [...]
Damn, maybe I should stop doing computer work and go be a teacher
heheh.
Thanks for the comments.
@Alex: sounds good. I’ll keep throwing in math stuff into the mix. I want to add more CompSci stuff anyway.
cheers
Awesome explanation, very entertaining. I look forward to more articles like this (new rss subscriber)!
@Gustavo: I’ve just done the reverse (Teacher -> Computer Scientist).
@Matt: welcome to the ranks
I really enjoy Math and CS, doing it, learning it, teaching it, anything. In fact, not just Math and CS, but anything analytical is pretty fun as well.
However I do get an extra kick from teaching because I think it’s such a positive thing to do in the world, whereas I can’t say the same about my paid computer work, and lately this has been on my mind (a la Tim O’Reilly’s Work on stuff that matters).
I’d like to move towards aligning my work with my ideals. But $ is a factor, as an independent developer my pay is well above what I’d get teaching, for example. We’ll see how it goes.
Great article. I’m not convinced by this line in your proof:
The digits of this number p are random and go on infinitely; it is a real number.
I agree that p can’t be in the list because we have constructed it such that it is not real. I fail to see any property of p that would require it to be real. So I reject the contradiction on the grounds that p is not a real number.
To complete the contradiction, you should trace its realness back to one of the real number construction methods (http://en.wikipedia.org/wiki/Construction_of_the_real_numbers). I’m not sure that that’s possible, because I suspect p is non-real. Not a mathematician though
Most excellent. Thank you.
Hi Gustavo, I just wanted to commend you on doing a fantastic job on this writeup. I’m a big fan of clear, intuitive explanations and I think approaching topics with analogies & humor is a great tactic. I’ve been personally interested in understanding infinity better, and am looking forward to the next article!
I would recommend watching Dangerous Knowledge: http://www.google.com/search?q=Dangerous%20Knowledge – it’s a BBC documentary on the fathers of modern mathematics:
“In this one-off documentary, David Malone looks at four brilliant mathematicians – Georg Cantor, Ludwig Boltzmann, Kurt Gödel and Alan Turing – whose genius has profoundly affected us, but which tragically drove them insane and eventually led to them all committing suicide.”
[...] Excelente artículo de Gustavo Duarte sobre infinitos. Habla de infinitos numerables, y muestra que el conjunto de los racionales lo es. El todo que equivale a la parte: los números racionales incluyen a los enteros y a cualquier número que puedas construir con una fracción, pero Cantor vio que puedes asociar un número entero a cada número racional, sin dejarte ninguno. Los dos conjuntos son infinitos y equivalentes —equipotentes es la forma correcta de decirlo— a pesar de que uno de ellos incluye al otro. [...]
Thank you all for the feedback.
@Drew: That is a really smart observation. In other uses of diagonalization, people make arguments very much like what you just made. For example, Turing does _exactly_ what you did with computable numbers by building a diagonal off a list of computable numbers, getting a resulting number, and showing that the resulting number is not computable.
However, in this specific case, by definition our number _is_ real. Here is what you said:
My question to you would be this: if p is not real, then what is it? Is there some other set you’re proposing?
It turns out that due to the way the reals are _defined_, they must contain our number, and any other number like it. If you write a program to generate a number whose digits are completely random, using a natural source for random bits, the result _by definition_ is a real number.
So basically, ‘every number is in the reals’, unless it’s imaginary (http://en.wikipedia.org/wiki/Imaginary_number). This is a crude way of expressing it of course, but it follows from the precise definitions of the reals.
The definition in question is that the reals are Dedekind-complete: http://en.wikipedia.org/wiki/Dedekind_completion.
Suppose our crazy random number P were NOT a real number. Then it would divide the reals in two sets, one set A of all reals less than our number, and one set B of all reals more than our number. But P itself would not be in A nor B. But this violates the property of Dedekind completeness, so P must be in the reals.
@Kalid: your site rocks, I have read many of your articles as well.
Again, thank you all for stopping by.
To Drew and Gustavo:
On the page mentioned by Drew
http://en.wikipedia.org/wiki/Construction_of_the_real_numbers
several constructions are mentioned from which it can easily be seen that p is (or rather defines a) real number:
one of the ways the real numbers are constructed is as equivalence classes of (or intuitively, limit of) Cauchy sequences of rational numbers. A sequence of decimal digits behind the decimal point really is (in this construction) the limit of its truncations, which is a Cauchy sequence of rational numbers. In fact, on that page it also mentions the construction as decimal expansions explicitly.
The construction by Dedekind cuts that Gustavo is referring to also is easy to apply: in this construction p stands for the Dedekind cut of the rationals defined as follows: given a rational number you can say whether it is greater or smaller than p by looking at its decimal expansion and comparing those (lexicographically).
Gustavo, I’m afraid your argument is not entirely watertight. Dedekind completeness means that if (A,B) is a Dedekind cut of the real numbers, then every real number is either contained in A or in B. If p is not a real number, there is no contradiction in p not being contained in either.
Correction: the last paragraph must be
If (A,B) is a Dedekind cut of the real numbers, by definition every real number is either contained in A or in B. If p is not a real number, there can be no contradiction in p not being contained in either.
(Dedekind completeness, meaning that B has a minimal element for every Dedekind cut, doesn’t enter the picture)
@Doetoe: thanks for stopping by. I’ve been meaning to get my math back in shape, so this is great discussion. Here’s a better write up on completeness and what I tried to say (but failed):
The rationals, reals and complex numbers are all ordered fields, roughly because they meet some criteria when it comes to addition, multiplication, and the relation < . So far so good.
Now take a subset A of an ordered field F (eg, subset 0 to 2, inclusive, of the rationals). If we have an element u in F such that a <= u for all a in A, then that element is an _upper bound_ for A. For [0,2], here are some examples of upper bounds: 2, 3, 2.5, 1000, etc.
But [0,2] has a special upper bound: 2. 2 is significant because it is an upper bound for [0,2] and it is <= _any other_ upper bound of [0,2]. 2 in this case is a _least upper bound_ or _supremum_ for [0,2].
More generally, if A is a subset of ordered field F, s in F is a _least upper bound_ for A if and only if: 1) s is an upper bound for A; 2) s <= t for all upper bounds t of A.
Now comes the rub: an ordered field F is _complete_ if and only if every nonempty subset of F that has an upper bound in F has a supremum that is also in F.
The rationals are NOT complete. For example, think of the subset of rationals A, x in A such that x >= 0 and x^2 < = 2. This subset has plenty of rational upper bounds. For example: 1.5, 2, 300, etc.
But it does NOT have a supremum in A. This is because fractions can always get closer and closer to the square root of 2, but they never reach it. So if you think you have a supremum s, it's always possible to come up with a fraction such that it is > s and < = square root of 2. Thus s wasn't a supremum after all. This can go on indifinitely.
The reals, on the other hand, are complete. We define them as such, either directly or by defining another property that implies completeness. They are 'the' complete field, in fact, because any two complete ordered fields are isomorphic.
So, in the case of the reals, this is what is going on: if the number p is NOT in the reals, I can define a subset A such that x in A: x < p. A has upper bounds in the reals, in fact any x > 1 is an upper bound for A due to how p was defined. However this subset does NOT have a supremum in the reals, because even though p is not in the reals, you can always approximate it a little further. But then, if this subset doesn’t have a supremum, the reals are NOT complete. This is a contradiction. Thus p is a real number, and it is indeed the supremum for A.
So basically, that was a long way to say that by definition p is in the reals
And now I want to go to grad school. hahah. Maybe I should take analysis in the fall.
Let’s say we define the set of all p-like numbers S (where each kth digit is not the kth digit of the kth real).
By the definition of the set S, to prove “p is real” it is necessary and sufficient to prove “S is the set of reals.”
To undertake this task, we must do the following:
1. Define a basic algebra on S.
2. Show the set S Archimedian
3. Show the set S complete.
None of these are trivial undertakings. If even one of them falls, the entire system falls.
What algebra are we defining in S? What would be the operation to add two elements of S, for instance? To multiply two elements of S?
We can make S Archimedian easy enough, simply by using a left alphabetic ordering:
1230…
…
1231…
…
1232…
…
1233…
…
1234…
…
1235…
…
1236…
…
1237…
…
1238…
Proof by contradiction: this ordering is incomplete. Assume the ordering we’ve described is complete. In that case, each subset of S would have a least upper bound in S. We define such a subset to be the numbers in the ordering above. That is, for t element of S, 1230000… < t < 12389999…
At this point we would have to invoke a little algebra to get a least upper bound. Surprisingly, that upper bound would be the number q = 12390000… Since each subset of S has a least upper bound in S, and since q is the least upper bound, q must be in S *
However, by the definition of S, the kth digit cannot be some number k. Since we have accepted [0,1,2,3,4,5,6,7,8] in the 4th digit for elements in S, by the definition of S, there cannot exist some number in S with 9 in the 4th digit. Since q has a 9 in the 4th digit, it cannot be in S*. Since q is in S and q is not in S, we have a contradiction. QED.
Drew,
Here is what I think are the two problems with the proof:
The first problem is the notion of the ‘kth’ real. There’s no such thing, _unless_ the reals are denumerable. So you’d have to prove that first before evoking the notion of kth real.
The second problem is stating that it is necessary to prove that S is the set of reals. It would indeed be sufficient, but it’s not necessary. S can be a _subset_ of the reals, hence not complete.
In fact, if you define some function mapping the naturals to the reals, such that the ‘kth’ real makes sense (the function would be non-surjective, assuming Cantor is right) and proceed to build set S, you’re right that S would not be complete.
That would not be due to the fact that the numbers in it aren’t reals, but just because S would be a subset of the reals that isn’t complete, much like the naturals or rationals.
Thank you very much.
its nice and very useful
Great post, I’ve been meaning to read about infinities for a while but never found something this concise and understandable. I only have one addition: Where you say “It differs in at least one digit.”, it would perhaps be helpful to explain *why* this is so. It was not immediately obvious to me, and I had to look it up in Wikipedia.
The answer, of course, is that if that number *were* on the list and was the Nth number, its Nth digit would be the red one, but we know that its Nth digit is different than the red one.
Is this forum a gathering place of idiots? Cantor was a fool and so I am not surprised.
Your (Cantor’s) argument is lame. Do you understand that by changing the elements on the diagonal that you still end up with a number that is in fact in the original list? This of course being true assuming that every real number in the interval (0,1) can be represented as a decimal…
@John: it is. Glad you stopped by!
Gustavo -
Excellent article. I’m not a mathematician but was introduced to the Cantor diagonal via Gödel, Escher, Bach. Anyway, I found in discussions with colleagues that it was necessary to be more explicit in the explanation. Something like:
You take the digits on the diagonal in the table and construct a(n infinitely long) “new” number, which one assumes would be found someone in the infinitely long list of reals since all real numbers are in the table. However, now you change each digit in our “new” number by adding or subtracting one, etc., to make a new digit, and hence a new number. Strangely, that number is nowhere in the list.
[Incredulity on the part of others. Huh? What?]
Well, the new number is not the same as the first number in the list because the first digit is different.
It’s not the same as the second number in the list because the second digit is different.
…
Anyway, I know that’s a bit long-winded, but most people need it spelled out explicity, at which point the light bulb goes on.
Cheers,
Charles
An excellent article, thank you very much!
My sister is quite puzzled. They started OK, and the support is hard to reach.