I hope the previous post explained virtual memory adequately, but I must admit I held back a much better explanation, which I first saw in Expert C Programming. It wasn't written by the book's author, Peter van der Linden, but rather by Jeff Berryman in 1972. Here goes:

The Thing King and the Paging Game

This note is a formal non-working paper of the Project MAC Computer Systems Research Division. It should be reproduced and distributed wherever levity is lacking, and may be referenced at your own risk in other publications.

Rules

1. Each player gets several million things.
2. Things are kept in crates that hold 4096 things each. Things in the same crate are called crate-mates.
3. Crates are stored either in the workshop or the warehouses. The workshop is almost always too small to hold all the crates.
4. There is only one workshop but there may be several warehouses. Everybody shares them.
5. Each thing has its own thing number.
6. What you do with a thing is to zark it. Everybody takes turns zarking.
7. You can only zark your things, not anybody else's.
8. Things can only be zarked when they are in the workshop.
9. Only the Thing King knows whether a thing is in the workshop or in a warehouse.
10. The longer a thing goes without being zarked, the grubbier it is said to become.
11. The way you get things is to ask the Thing King. He only gives out things by the crateful. This is to keep the royal overhead down.
12. The way you zark a thing is to give its thing number. If you give the number of a thing that happens to be in a workshop it gets zarked right away. If it is in a warehouse, the Thing King packs the crate containing your thing back into the workshop. If there is no room in the workshop, he first finds the grubbiest crate in the workshop, whether it be yours or somebody else's, and packs it off with all its crate-mates to a warehouse. In its place he puts the crate containing your thing. Your thing then gets zarked and you never know that it wasn't in the workshop all along.
13. Each player's stock of things have the same numbers as everybody else's. The Thing King always knows who owns what thing and whose turn it is, so you can't ever accidentally zark somebody else's thing even if it has the same thing number as one of yours.

Notes

1. Traditionally, the Thing King sits at a large, segmented table and is attended to by pages (the so-called "table pages") whose job it is to help the king remember where all the things are and who they belong to.
2. One consequence of Rule 13 is that everybody's thing numbers will be similar from game to game, regardless of the number of players.
3. The Thing King has a few things of his own, some of which move back and forth between workshop and warehouse just like anybody else's, but some of which are just too heavy to move out of the workshop.
4. With the given set of rules, oft-zarked things tend to get kept mostly in the workshop while little-zarked things stay mostly in a warehouse. This is efficient stock control.

Long Live the Thing King!

Update: Alex pointed out the difficulties of measuring grubbiness in a comment below.

14 Comments

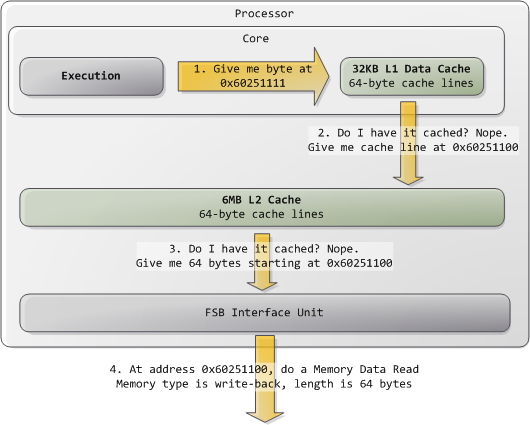
After examining the virtual address layout of a process, we turn to the kernel and its mechanisms for managing user memory. Here is gonzo again:

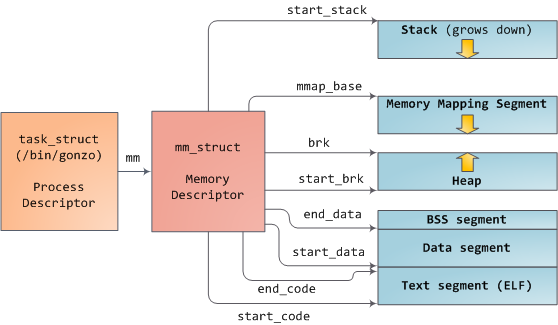
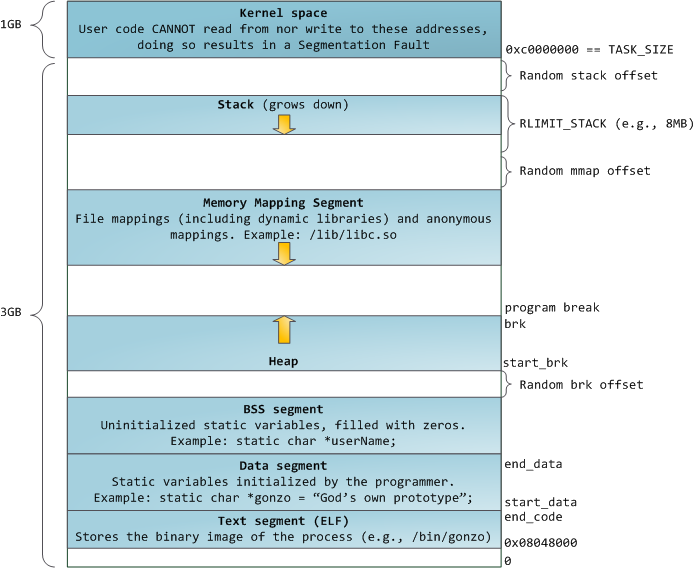
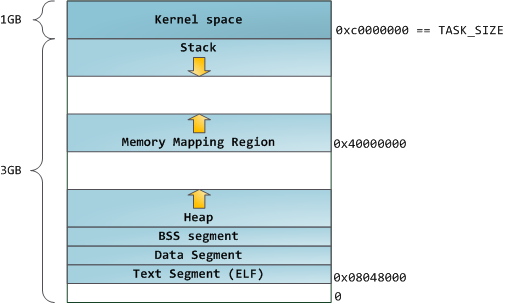
Linux processes are implemented in the kernel as instances of task_struct, the process descriptor. The mm field in task_struct points to the memory descriptor, mm_struct, which is an executive summary of a program's memory. It stores the start and end of memory segments as shown above, the number of physical memory pages used by the process (rss stands for Resident Set Size), the amount of virtual address space used, and other tidbits. Within the memory descriptor we also find the two work horses for managing program memory: the set of virtual memory areas and the page tables. Gonzo's memory areas are shown below:

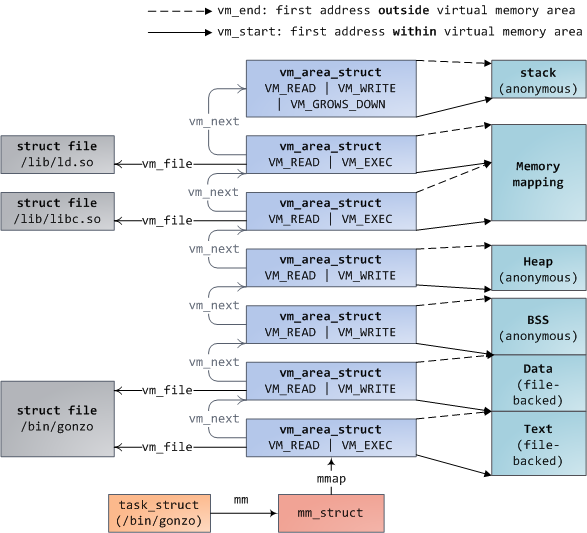
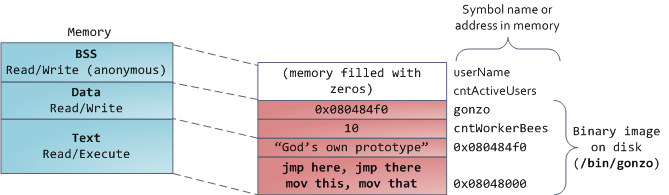
Each virtual memory area (VMA) is a contiguous range of virtual addresses; these areas never overlap. An instance of vm_area_struct fully describes a memory area, including its start and end addresses, flags to determine access rights and behaviors, and the vm_file field to specify which file is being mapped by the area, if any. A VMA that does not map a file is anonymous. Each memory segment above (e.g., heap, stack) corresponds to a single VMA, with the exception of the memory mapping segment. This is not a requirement, though it is usual in x86 machines. VMAs do not care which segment they are in.

A program's VMAs are stored in its memory descriptor both as a linked list in the mmap field, ordered by starting virtual address, and as a red-black tree rooted at the mm_rb field. The red-black tree allows the kernel to search quickly for the memory area covering a given virtual address. When you read file /proc/pid_of_process/maps, the kernel is simply going through the linked list of VMAs for the process and printing each one.

In Windows, the EPROCESS block is roughly a mix of task_struct and mm_struct. The Windows analog to a VMA is the Virtual Address Descriptor, or VAD; they are stored in an AVL tree. You know what the funniest thing about Windows and Linux is? It's the little differences.

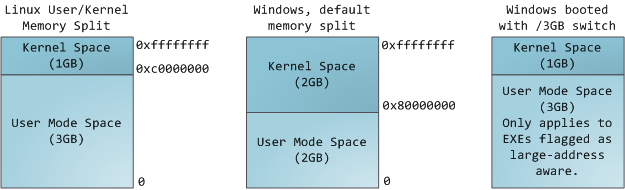
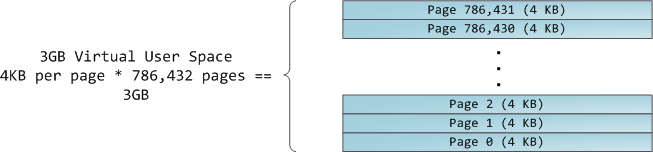
The 4GB virtual address space is divided into pages. x86 processors in 32-bit mode support page sizes of 4KB, 2MB, and 4MB. Both Linux and Windows map the user portion of the virtual address space using 4KB pages. Bytes 0-4095 fall in page 0, bytes 4096-8191 fall in page 1, and so on. The size of a VMA must be a multiple of page size. Here's 3GB of user space in 4KB pages:

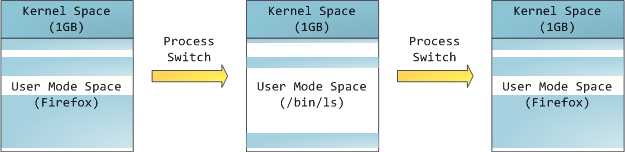
The processor consults page tables to translate a virtual address into a physical memory address. Each process has its own set of page tables; whenever a process switch occurs, page tables for user space are switched as well. Linux stores a pointer to a process' page tables in the pgd field of the memory descriptor. To each virtual page there corresponds one page table entry (PTE) in the page tables, which in regular x86 paging is a simple 4-byte record shown below:

Linux has functions to read and set each flag in a PTE. Bit P tells the processor whether the virtual page is present in physical memory. If clear (equal to 0), accessing the page triggers a page fault. Keep in mind that when this bit is zero, the kernel can do whatever it pleases with the remaining fields. The R/W flag stands for read/write; if clear, the page is read-only. Flag U/S stands for user/supervisor; if clear, then the page can only be accessed by the kernel. These flags are used to implement the read-only memory and protected kernel space we saw before.

Bits D and A are for dirty and accessed. A dirty page has had a write, while an accessed page has had a write or read. Both flags are sticky: the processor only sets them, they must be cleared by the kernel. Finally, the PTE stores the starting physical address that corresponds to this page, aligned to 4KB. This naive-looking field is the source of some pain, for it limits addressable physical memory to 4 GB. The other PTE fields are for another day, as is Physical Address Extension.

A virtual page is the unit of memory protection because all of its bytes share the U/S and R/W flags. However, the same physical memory could be mapped by different pages, possibly with different protection flags. Notice that execute permissions are nowhere to be seen in the PTE. This is why classic x86 paging allows code on the stack to be executed, making it easier to exploit stack buffer overflows (it's still possible to exploit non-executable stacks using return-to-libc and other techniques). This lack of a PTE no-execute flag illustrates a broader fact: permission flags in a VMA may or may not translate cleanly into hardware protection. The kernel does what it can, but ultimately the architecture limits what is possible.

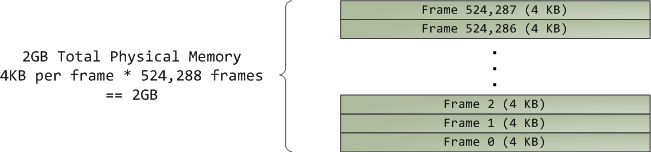
Virtual memory doesn't store anything, it simply maps a program's address space onto the underlying physical memory, which is accessed by the processor as a large block called the physical address space. While memory operations on the bus are somewhat involved, we can ignore that here and assume that physical addresses range from zero to the top of available memory in one-byte increments. This physical address space is broken down by the kernel into page frames. The processor doesn't know or care about frames, yet they are crucial to the kernel because the page frame is the unit of physical memory management. Both Linux and Windows use 4KB page frames in 32-bit mode; here is an example of a machine with 2GB of RAM:

In Linux each page frame is tracked by a descriptor and several flags. Together these descriptors track the entire physical memory in the computer; the precise state of each page frame is always known. Physical memory is managed with the buddy memory allocation technique, hence a page frame is free if it's available for allocation via the buddy system. An allocated page frame might be anonymous, holding program data, or it might be in the page cache, holding data stored in a file or block device. There are other exotic page frame uses, but leave them alone for now. Windows has an analogous Page Frame Number (PFN) database to track physical memory.

Let's put together virtual memory areas, page table entries and page frames to understand how this all works. Below is an example of a user heap:

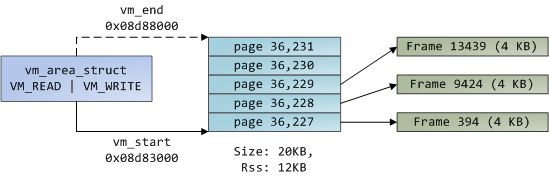
Blue rectangles represent pages in the VMA range, while arrows represent page table entries mapping pages onto page frames. Some virtual pages lack arrows; this means their corresponding PTEs have the Present flag clear. This could be because the pages have never been touched or because their contents have been swapped out. In either case access to these pages will lead to page faults, even though they are within the VMA. It may seem strange for the VMA and the page tables to disagree, yet this often happens.

A VMA is like a contract between your program and the kernel. You ask for something to be done (memory allocated, a file mapped, etc.), the kernel says "sure", and it creates or updates the appropriate VMA. But it does not actually honor the request right away, it waits until a page fault happens to do real work. The kernel is a lazy, deceitful sack of scum; this is the fundamental principle of virtual memory. It applies in most situations, some familiar and some surprising, but the rule is that VMAs record what has been agreed upon, while PTEs reflect what has actually been done by the lazy kernel. These two data structures together manage a program's memory; both play a role in resolving page faults, freeing memory, swapping memory out, and so on. Let's take the simple case of memory allocation:

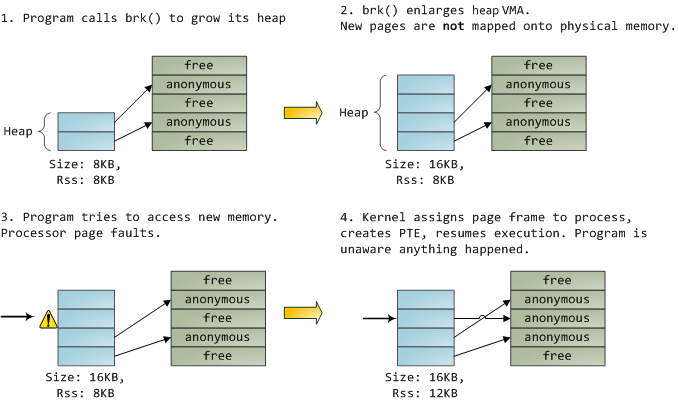
When the program asks for more memory via the brk() system call, the kernel simply updates the heap VMA and calls it good. No page frames are actually allocated at this point and the new pages are not present in physical memory. Once the program tries to access the pages, the processor page faults and do_page_fault() is called. It searches for the VMA covering the faulted virtual address using find_vma(). If found, the permissions on the VMA are also checked against the attempted access (read or write). If there's no suitable VMA, no contract covers the attempted memory access and the process is punished by Segmentation Fault.

When a VMA is found the kernel must handle the fault by looking at the PTE contents and the type of VMA. In our case, the PTE shows the page is not present. In fact, our PTE is completely blank (all zeros), which in Linux means the virtual page has never been mapped. Since this is an anonymous VMA, we have a purely RAM affair that must be handled by do_anonymous_page(), which allocates a page frame and makes a PTE to map the faulted virtual page onto the freshly allocated frame.

Things could have been different. The PTE for a swapped out page, for example, has 0 in the Present flag but is not blank. Instead, it stores the swap location holding the page contents, which must be read from disk and loaded into a page frame by do_swap_page() in what is called a major fault.

This concludes the first half of our tour through the kernel's user memory management. In the next post, we'll throw files into the mix to build a complete picture of memory fundamentals, including consequences for performance.

124 Comments

Memory management is the heart of operating systems; it is crucial for both programming and system administration. In the next few posts I'll cover memory with an eye towards practical aspects, but without shying away from internals. While the concepts are generic, examples are mostly from Linux and Windows on 32-bit x86. This first post describes how programs are laid out in memory.

Each process in a multi-tasking OS runs in its own memory sandbox. This sandbox is the virtual address space, which in 32-bit mode is always a 4GB block of memory addresses. These virtual addresses are mapped to physical memory by page tables, which are maintained by the operating system kernel and consulted by the processor. Each process has its own set of page tables, but there is a catch. Once virtual addresses are enabled, they apply to all software running in the machine, including the kernel itself. Thus a portion of the virtual address space must be reserved to the kernel:

This does not mean the kernel uses that much physical memory, only that it has that portion of address space available to map whatever physical memory it wishes. Kernel space is flagged in the page tables as exclusive to privileged code (ring 2 or lower), hence a page fault is triggered if user-mode programs try to touch it. In Linux, kernel space is constantly present and maps the same physical memory in all processes. Kernel code and data are always addressable, ready to handle interrupts or system calls at any time. By contrast, the mapping for the user-mode portion of the address space changes whenever a process switch happens:

Blue regions represent virtual addresses that are mapped to physical memory, whereas white regions are unmapped. In the example above, Firefox has used far more of its virtual address space due to its legendary memory hunger. The distinct bands in the address space correspond to memory segments like the heap, stack, and so on. Keep in mind these segments are simply a range of memory addresses and have nothing to do with Intel-style segments. Anyway, here is the standard segment layout in a Linux process:

When computing was happy and safe and cuddly, the starting virtual addresses for the segments shown above were exactly the same for nearly every process in a machine. This made it easy to exploit security vulnerabilities remotely. An exploit often needs to reference absolute memory locations: an address on the stack, the address for a library function, etc. Remote attackers must choose this location blindly, counting on the fact that address spaces are all the same. When they are, people get pwned. Thus address space randomization has become popular. Linux randomizes the stack, memory mapping segment, and heap by adding offsets to their starting addresses. Unfortunately the 32-bit address space is pretty tight, leaving little room for randomization and hampering its effectiveness.

The topmost segment in the process address space is the stack, which stores local variables and function parameters in most programming languages. Calling a method or function pushes a new stack frame onto the stack. The stack frame is destroyed when the function returns. This simple design, possible because the data obeys strict LIFO order, means that no complex data structure is needed to track stack contents - a simple pointer to the top of the stack will do. Pushing and popping are thus very fast and deterministic. Also, the constant reuse of stack regions tends to keep active stack memory in the cpu caches, speeding up access. Each thread in a process gets its own stack.

It is possible to exhaust the area mapping the stack by pushing more data than it can fit. This triggers a page fault that is handled in Linux by expand_stack(), which in turn calls acct_stack_growth() to check whether it's appropriate to grow the stack. If the stack size is below RLIMIT_STACK (usually 8MB), then normally the stack grows and the program continues merrily, unaware of what just happened. This is the normal mechanism whereby stack size adjusts to demand. However, if the maximum stack size has been reached, we have a stack overflow and the program receives a Segmentation Fault. While the mapped stack area expands to meet demand, it does not shrink back when the stack gets smaller. Like the federal budget, it only expands.

Dynamic stack growth is the only situation in which access to an unmapped memory region, shown in white above, might be valid. Any other access to unmapped memory triggers a page fault that results in a Segmentation Fault. Some mapped areas are read-only, hence write attempts to these areas also lead to segfaults.

Below the stack, we have the memory mapping segment. Here the kernel maps contents of files directly to memory. Any application can ask for such a mapping via the Linux mmap() system call (implementation) or CreateFileMapping() / MapViewOfFile() in Windows. Memory mapping is a convenient and high-performance way to do file I/O, so it is used for loading dynamic libraries. It is also possible to create an anonymous memory mapping that does not correspond to any files, being used instead for program data. In Linux, if you request a large block of memory via malloc(), the C library will create such an anonymous mapping instead of using heap memory. 'Large' means larger than MMAP_THRESHOLD bytes, 128 kB by default and adjustable via mallopt().

Speaking of the heap, it comes next in our plunge into address space. The heap provides runtime memory allocation, like the stack, meant for data that must outlive the function doing the allocation, unlike the stack. Most languages provide heap management to programs. Satisfying memory requests is thus a joint affair between the language runtime and the kernel. In C, the interface to heap allocation is malloc() and friends, whereas in a garbage-collected language like C# the interface is the new keyword.

If there is enough space in the heap to satisfy a memory request, it can be handled by the language runtime without kernel involvement. Otherwise the heap is enlarged via the brk() system call (implementation) to make room for the requested block. Heap management is complex, requiring sophisticated algorithms that strive for speed and efficient memory usage in the face of our programs' chaotic allocation patterns. The time needed to service a heap request can vary substantially. Real-time systems have special-purpose allocators to deal with this problem. Heaps also become fragmented, shown below:

Finally, we get to the lowest segments of memory: BSS, data, and program text. Both BSS and data store contents for static (global) variables in C. The difference is that BSS stores the contents of uninitialized static variables, whose values are not set by the programmer in source code. The BSS memory area is anonymous: it does not map any file. If you say static int cntActiveUsers, the contents of cntActiveUsers live in the BSS.

The data segment, on the other hand, holds the contents for static variables initialized in source code. This memory area is not anonymous. It maps the part of the program's binary image that contains the initial static values given in source code. So if you say static int cntWorkerBees = 10, the contents of cntWorkerBees live in the data segment and start out as 10. Even though the data segment maps a file, it is a private memory mapping, which means that updates to memory are not reflected in the underlying file. This must be the case, otherwise assignments to global variables would change your on-disk binary image. Inconceivable!

The data example in the diagram is trickier because it uses a pointer. In that case, the contents of pointer gonzo - a 4-byte memory address - live in the data segment. The actual string it points to does not, however. The string lives in the text segment, which is read-only and stores all of your code in addition to tidbits like string literals. The text segment also maps your binary file in memory, but writes to this area earn your program a Segmentation Fault. This helps prevent pointer bugs, though not as effectively as avoiding C in the first place. Here's a diagram showing these segments and our example variables:

You can examine the memory areas in a Linux process by reading the file /proc/pid_of_process/maps. Keep in mind that a segment may contain many areas. For example, each memory mapped file normally has its own area in the mmap segment, and dynamic libraries have extra areas similar to BSS and data. The next post will clarify what 'area' really means. Also, sometimes people say "data segment" meaning all of data + bss + heap.

You can examine binary images using the nm and objdump commands to display symbols, their addresses, segments, and so on. Finally, the virtual address layout described above is the "flexible" layout in Linux, which has been the default for a few years. It assumes that we have a value for RLIMIT_STACK. When that's not the case, Linux reverts back to the "classic" layout shown below:

That's it for virtual address space layout. The next post discusses how the kernel keeps track of these memory areas. Coming up we'll look at memory mapping, how file reading and writing ties into all this and what memory usage figures mean.

189 Comments

When trying to understand complex systems, you can often learn a lot by stripping away abstractions and looking at their lowest levels. In that spirit we take a look at memory and I/O ports in their simplest and most fundamental level: the interface between the processor and bus. These details underlie higher level topics like thread synchronization and the need for the Core i7. Also, since I'm a programmer I ignore things EE people care about. Here's our friend the Core 2 again:

A Core 2 processor has 775 pins, about half of which only provide power and carry no data. Once you group the pins by functionality, the physical interface to the processor is surprisingly simple. The diagram shows the key pins involved in a memory or I/O port operation: address lines, data pins, and request pins. These operations take place in the context of a transaction on the front side bus. FSB transactions go through 5 phases: arbitration, request, snoop, response, and data. Throughout these phases, different roles are played by the components on the FSB, which are called agents. Normally the agents are all the processors plus the northbridge.

We only look at the request phase in this post, in which 2 packets are output by the request agent, who is usually a processor. Here are the juiciest bits of the first packet, output by the address and request pins:

The address lines output the starting physical memory address for the transaction. We have 33 bits but they are interpreted as bits 35-3 of an address in which bits 2-0 are zero. Hence we have a 36-bit address, aligned to 8 bytes, for a total of 64GB addressable physical memory. This has been the case since the Pentium Pro. The request pins specify what type of transaction is being initiated; in I/O requests the address pins specify an I/O port rather than a memory address. After the first packet is output, the same pins transmit a second packet in the subsequent bus clock cycle:

The attribute signals are interesting: they reflect the 5 types of memory caching behavior available in Intel processors. By putting this information on the FSB, the request agent lets other processors know how this transaction affects their caches, and how the memory controller (northbridge) should behave. The processor determines the type of a given memory region mainly by looking at page tables, which are maintained by the kernel.

Typically kernels treat all RAM memory as write-back, which yields the best performance. In write-back mode the unit of memory access is the cache line, 64 bytes in the Core 2. If a program reads a single byte in memory, the processor loads the whole cache line that contains that byte into the L2 and L1 caches. When a program writes to memory, the processor only modifies the line in the cache, but does not update main memory. Later, when it becomes necessary to post the modified line to the bus, the whole cache line is written at once. So most requests have 11 in their length field, for 64 bytes. Here's a read example in which the data is not in the caches:

Some of the physical memory range in an Intel computer is mapped to devices like hard drives and network cards instead of actual RAM memory. This allows drivers to communicate with their devices by writing to and reading from memory. The kernel marks these memory regions as uncacheable in the page tables. Accesses to uncacheable memory regions are reproduced in the bus exactly as requested by a program or driver. Hence it's possible to read or write single bytes, words, and so on. This is done via the byte enable mask in packet B above.

The primitives discussed here have many implications. For example:

1. Performance-sensitive applications should try to pack data that is accessed together into the same cache line. Once the cache line is loaded, further reads are much faster and extra RAM accesses are avoided.
2. Any memory access that falls within a single cache line is guaranteed to be atomic (assuming write-back memory). Such an access is serviced by the processor's L1 cache and the data is read or written all at once; it cannot be affected halfway by other processors or threads. In particular, 32-bit and 64-bit operations that don't cross cache line boundaries are atomic.
3. The front bus is shared by all agents, who must arbitrate for bus ownership before they can start a transaction. Moreover, all agents must listen to all transactions in order to maintain cache coherence. Thus bus contention becomes a severe problem as more cores and processors are added to Intel computers. The Core i7 solves this by having processors attached directly to memory and communicating in a point-to-point rather than broadcast fashion.

These are the highlights of physical memory requests; the bus will surface again later in connection with locking, multi-threading, and cache coherence. The first time I saw FSB packet descriptions I had a huge "ahhh!" moment so I hope someone out there gets the same benefit. In the next post we'll go back up the abstraction ladder to take a thorough look at virtual memory.

[22 Comments](/comments/physical-memory.html)

This post shows briefly how CPU caches are organized in modern Intel processors. Cache discussions often lack concrete examples, obfuscating the simple concepts involved. Or maybe my pretty little head is slow. At any rate, here's half the story on how a Core 2 L1 cache is accessed:

The unit of data in the cache is the line, which is just a contiguous chunk of bytes in memory. This cache uses 64-byte lines. The lines are stored in cache banks or ways, and each way has a dedicated directory to store its housekeeping information. You can imagine each way and its directory as columns in a spreadsheet, in which case the rows are the sets. Then each cell in the way column contains a cache line, tracked by the corresponding cell in the directory. This particular cache has 64 sets and 8 ways, hence 512 cells to store cache lines, which adds up to 32KB of space.

In this cache's view of the world, physical memory is divided into 4KB physical pages. Each page has 4KB / 64 bytes == 64 cache lines in it. When you look at a 4KB page, bytes 0 through 63 within that page are in the first cache line, bytes 64-127 in the second cache line, and so on. The pattern repeats for each page, so the 3rd line in page 0 is different than the 3rd line in page 1.

In a fully associative cache any line in memory can be stored in any of the cache cells. This makes storage flexible, but it becomes expensive to search for cells when accessing them. Since the L1 and L2 caches operate under tight constraints of power consumption, physical space, and speed, a fully associative cache is not a good trade off in most scenarios.

Instead, this cache is set associative, which means that a given line in memory can only be stored in one specific set (or row) shown above. So the first line of any physical page (bytes 0-63 within a page) must be stored in row 0, the second line in row 1, etc. Each row has 8 cells available to store the cache lines it is associated with, making this an 8-way associative set. When looking at a memory address, bits 11-6 determine the line number within the 4KB page and therefore the set to be used. For example, physical address 0x800010a0 has 000010 in those bits so it must be stored in set 2.

But we still have the problem of finding which cell in the row holds the data, if any. That's where the directory comes in. Each cached line is tagged by its corresponding directory cell; the tag is simply the number for the page where the line came from. The processor can address 64GB of physical RAM, so there are 64GB / 4KB == 2²⁴ of these pages and thus we need 24 bits for our tag. Our example physical address 0x800010a0 corresponds to page number 524,289. Here's the second half of the story:

Since we only need to look in one set of 8 ways, the tag matching is very fast; in fact, electrically all tags are compared simultaneously, which I tried to show with the arrows. If there's a valid cache line with a matching tag, we have a cache hit. Otherwise, the request is forwarded to the L2 cache, and failing that to main system memory. Intel builds large L2 caches by playing with the size and quantity of the ways, but the design is the same. For example, you could turn this into a 64KB cache by adding 8 more ways. Then increase the number of sets to 4096 and each way can store 256KB. These two modifications would deliver a 4MB L2 cache. In this scenario, you'd need 18 bits for the tags and 12 for the set index; the physical page size used by the cache is equal to its way size.

If a set fills up, then a cache line must be evicted before another one can be stored. To avoid this, performance-sensitive programs try to organize their data so that memory accesses are evenly spread among cache lines. For example, suppose a program has an array of 512-byte objects such that some objects are 4KB apart in memory. Fields in these objects fall into the same lines and compete for the same cache set. If the program frequently accesses a given field (e.g., the vtable by calling a virtual method), the set will likely fill up and the cache will start trashing as lines are repeatedly evicted and later reloaded. Our example L1 cache can only hold the vtables for 8 of these objects due to set size. This is the cost of the set associativity trade-off: we can get cache misses due to set conflicts even when overall cache usage is not heavy. However, due to the relative speeds in a computer, most apps don't need to worry about this anyway.

A memory access usually starts with a linear (virtual) address, so the L1 cache relies on the paging unit to obtain the physical page address used for the cache tags. By contrast, the set index comes from the least significant bits of the linear address and is used without translation (bits 11-6 in our example). Hence the L1 cache is physically tagged but virtually indexed, helping the CPU to parallelize lookup operations. Because the L1 way is never bigger than an MMU page, a given physical memory location is guaranteed to be associated with the same set even with virtual indexing. L2 caches, on the other hand, must be physically tagged and physically indexed because their way size can be bigger than MMU pages. But then again, by the time a request gets to the L2 cache the physical address was already resolved by the L1 cache, so it works out nicely.

Finally, a directory cell also stores the state of its corresponding cached line. A line in the L1 code cache is either Invalid or Shared (which means valid, really). In the L1 data cache and the L2 cache, a line can be in any of the 4 MESI states: Modified, Exclusive, Shared, or Invalid. Intel caches are inclusive: the contents of the L1 cache are duplicated in the L2 cache. These states will play a part in later posts about threading, locking, and that kind of stuff. Next time we'll look at the front side bus and how memory access really works. This is going to be memory week.

Update: Dave brought up direct-mapped caches in a comment below. They’re basically a special case of set-associative caches that have only one way. In the trade-off spectrum, they’re the opposite of fully associative caches: blazing fast access, lots of conflict misses.

26 Comments